基尼系数及其由来(0711)
基尼系数及其由来(0711)
基尼系数
1.基尼系数是什么?
基尼系数:是用来衡量一个国家或地区居民收入差距的指标。
换句话说,就是一个国家或地区居民贫富差距的指数。
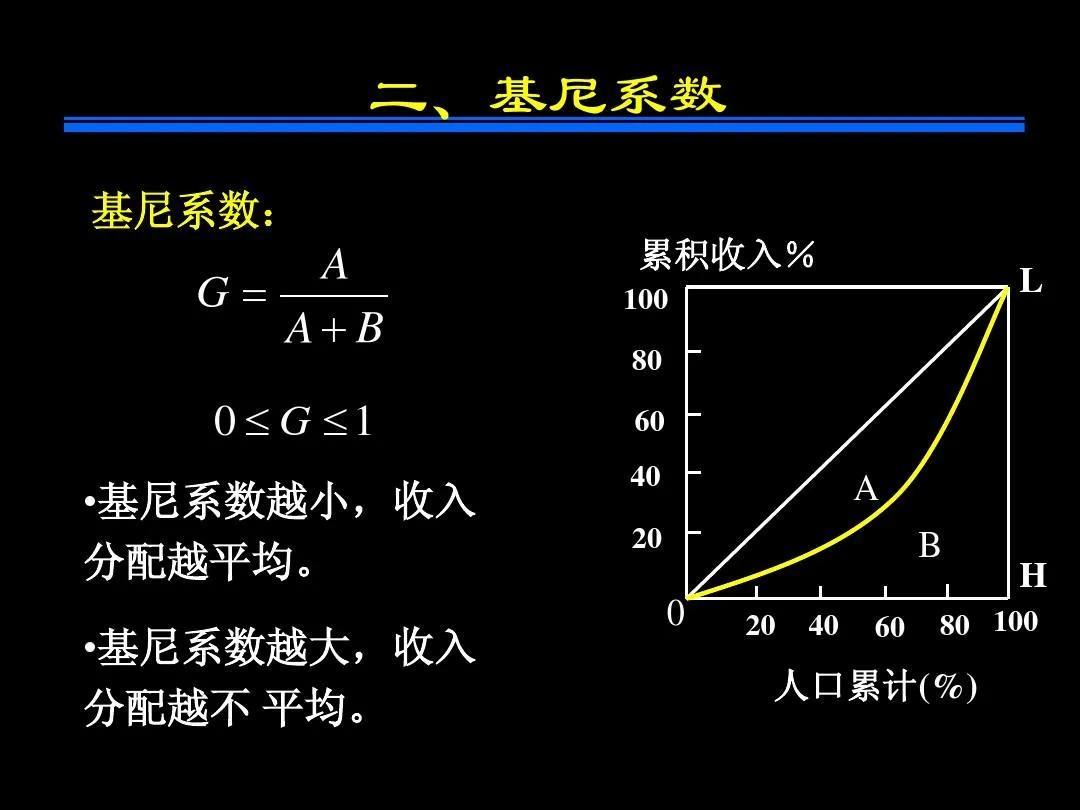
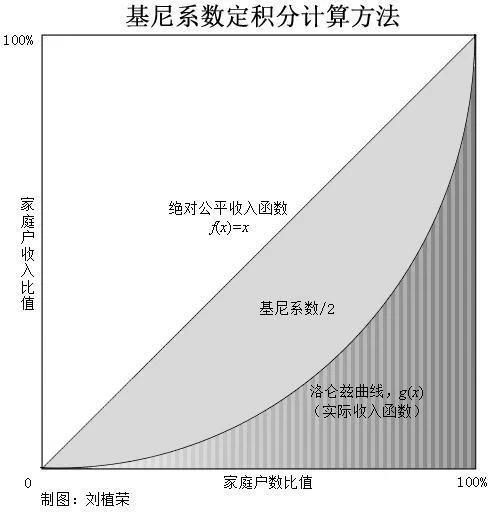
2.如何计算基尼系数?
现在举例说明。
假设,某一地区有人口1万,总收入为1亿元。平均收入:
100,000,000元÷10,000
=10,000元
假定,以上数据不变。
①第一种情况,将1亿元全部平均分发给这1万人,每人可以得到1万元。
问题:有没有不平均分配?如果有,不平均分配金额是多少?
回答:没有不平均分配。由于总金额是1亿元,不平均分配金额为0元。不平均分配金额与总收入的比就是:
0÷100,000,000=0
这个比值,就叫做基尼系数,等于0。
(这表明居民收入相同。)
②第二种情况,将1亿元分成两部分:一份是9千万元,另一份是1千万元。
首先,将第一份9千万元平均分配给这1万人。每人可以分到9千元。
接着,将另一份1千万元作不平均分配。有的人可以得到很多,有的人得到的很少,甚至没有。
这个进行不平均分配的1千万元与总收入1亿元的比值是:
10,000,000÷100,000,000
=0.1
这个比值,也就是基尼系数,等于0.1。
(这表明居民收入略有不同。)
③第三种情况,将1亿元分成两部分:一份是8千万元,另一份是2千万元。
首先,将第一份8千万元平均分配给这1万人。每人可以分到8千元。
接着,将另一份2千万元作不平均分配。有的人可以得到很多,有的人得到的很少,甚至没有。
这个进行不平均分配的2千万元与总收入1亿元的比值是:
20,000,000÷100,000,000
=0.2
这个比值,也就是基尼系数,等于0.2。
(这表明居民收入稍有不同。)
以此类推,基尼系数可以从0开始变大:0.1,0.2,0.3 ......(也可以是其他小于1的小数。)
④第四种情况,将1亿元分成两部分:一份是0千万元,另一份是10千万元(也就是1亿元)。
首先,将第一份0千万元平均分配给这1万人。每人可以分到0元。
接着,将另一份10千万元作不平均分配。有的人可以得到很多,有的人得到的很少,甚至没有。
这个进行不平均分配的10千万元(即1亿元)与总收入1亿元的比值是:
100,000,000÷100,000,000
=1
这个比值,也就是基尼系数,等于1。
(这表明居民收入非常悬殊。)
基尼系数在0和1之间。也就是说,基尼系数的最小值是0,最大值是1。
3.基尼系数的意义。
基尼系数:是用来衡量一个国家或地区居民收入差距的指标。
它表示在全部居民收入中,用于进行不平均分配的那部分收入与总收入的比值。
4.基尼系数的由来。
基尼系数,最早由意大利统计与社会学家克拉多·基尼(Corrado Gini)在1912年提出。

5.小结。
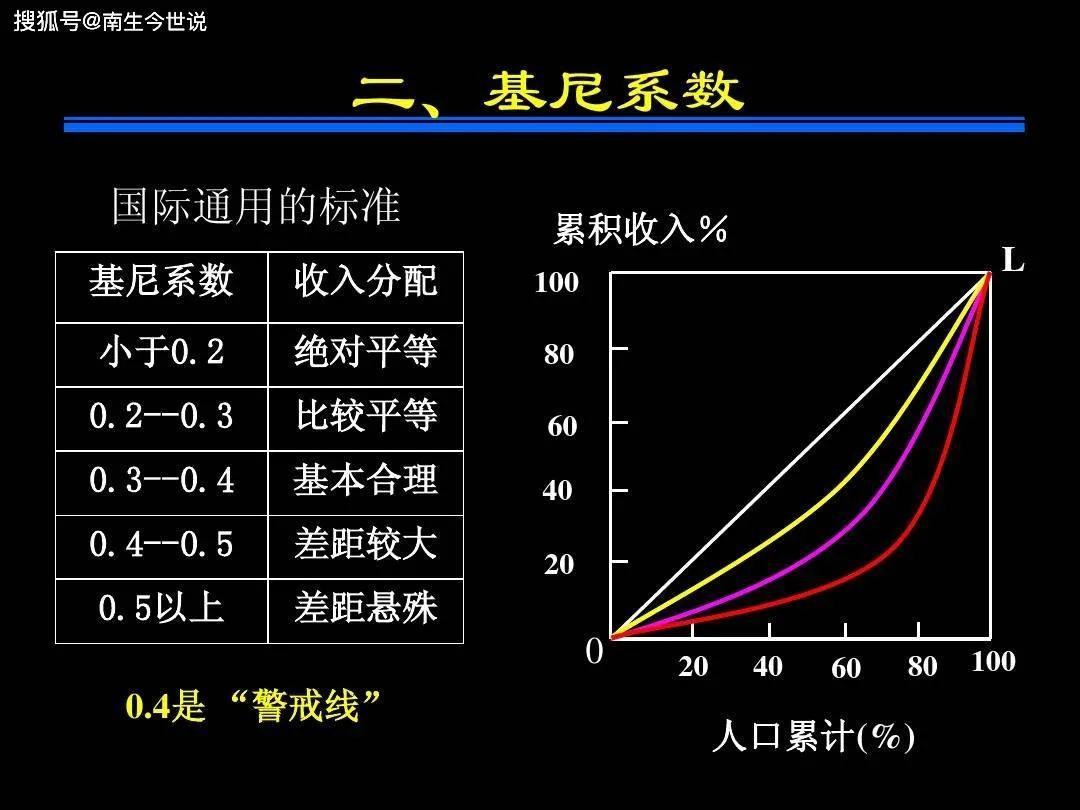
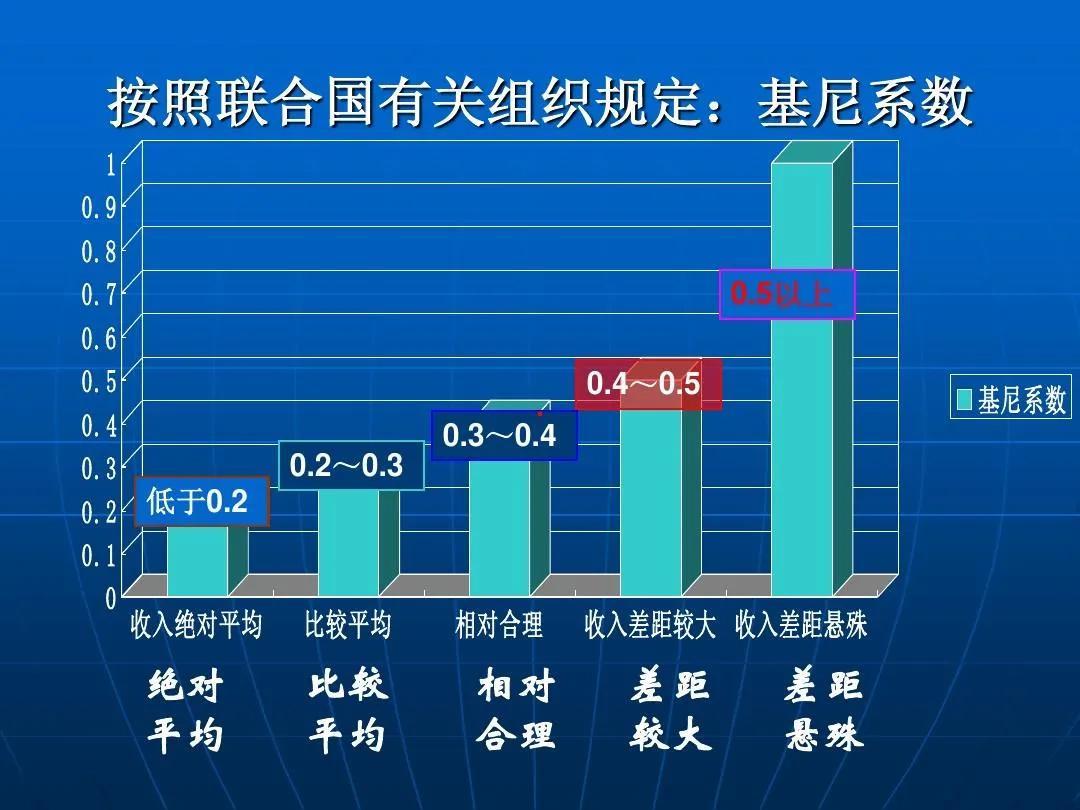
国际上,联合国有关组织认为:
基尼系数小于0.2时,居民收入过于平均,
0.2-0.3之间时较为平均,
0.3-0.4之间时比较合理,
0.4-0.5时差距过大,
大于0.5时差距悬殊。
普通常识,温故知新。
轻松浏览,无需点评。
-

- 郑大体院要自立门户,二本分再也上不了211了,学生欲哭无泪
-
2025-06-11 01:41:42
-

- 五爷的责任田
-
2025-06-11 01:39:26
-
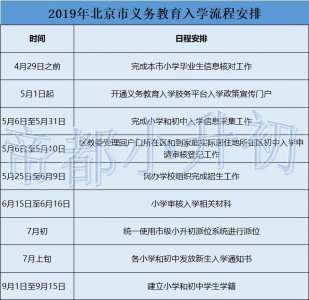
- 北京16区小升初入学流程超全汇总!关键时间点都理好了!
-
2025-06-11 01:37:11
-

- 重温《鲁冰花》:当熟悉的旋律响起,我已经开始想哭了
-
2025-06-11 01:34:55
-

- 有心了!T-ara成员发文庆祝出道11周年,“巨魔事件”又引发讨论
-
2025-06-11 01:32:39
-

- 甜品店十大品牌排行榜,DQ仅排第五,第一专注于制作港式甜品
-
2025-06-11 01:30:23
-

- 夜场“吹气球”上瘾,“笑气”会给人带来哪些伤害?
-
2025-06-11 01:28:08
-

- 国行switch已经开售,选国行还是海外版?别慌,我们一一比较
-
2025-06-11 01:25:53
-

- 希言自然
-
2025-06-11 01:23:38
-

- 年底遭解雇或跳槽,社保、工资、年休假、年终奖该怎么处理?
-
2025-06-11 01:21:23
-

- 鸽子蛋2元钱一枚,养殖户坦言赔惨了,农村大爷成接盘侠
-
2025-06-11 01:19:08
-

- 著名女打星元秋有多厉害?成龙敬她三分,周星驰低声下气求出山
-
2025-06-11 01:16:53
-

- 我的世界:聊聊实体303背后的谜团,揭开我的世界秘密的关键?
-
2025-06-11 01:14:38
-

- 黑色四叶草209话:复活二人组即将领便当,阿斯塔和尤诺身世曝光
-
2025-06-11 01:12:23
-

- 攸佳宁一人撑起《最强大脑》第七季,这档智力比拼节目会走向何方
-
2025-06-11 01:10:08
-

- 四大名师的传奇忠告:鞭亡而亡的尉迟恭,兄弟不分离的岳飞四兄弟
-
2025-06-11 01:07:53
-

- 鲸为什么会搁浅?这是一种习性吗?
-
2025-06-11 01:05:38
-

- SWIFT是什么?对全球贸易影响几何?
-
2025-06-11 01:03:22
-

- 余文乐曾为阿SA与陈冠希开撕,至今14年恩怨,现在沉底了?
-
2025-06-11 01:01:07
-
- 西瓜商城网 - 国内优秀的网站源码网,内含大量免费源码程序
-
2025-06-10 08:08:39


 许凯妈妈旧照,看到他妈妈年轻时的样子,才知道他为啥这么帅气
许凯妈妈旧照,看到他妈妈年轻时的样子,才知道他为啥这么帅气 丰田推出的倒三轮摩托车,只要1万多,可惜国内没有卖的
丰田推出的倒三轮摩托车,只要1万多,可惜国内没有卖的